Übungsaufgaben
zur Mathematik
in 11.2
Zur Bearbeitung
der folgenden Aufgaben haben Sie ca. 180 Minuten!
Hilfsmittel:
nichtprogrammierbarer Taschenrechner,
Formelsammlung mit handschriftlichen
Ergänzungen.
Hinweis:
Zur korrekten
Darstellung muss in Ihrem Browser ein Unicode-Zeichensatz eingestellt
sein!
1. Gegeben
sind die Mengen A = { 2, 4, 6, 8 }
und B = { +,
-, *, / }.
Geben Sie je eine Relation R ∈ A x B in
aufzählender Form an, die
a) rechtstotal und linkseindeutig ist,
b) rechtseindeutig, linkstotal und rechtstotal ist,
c) links- und rechtstotal, aber weder links- noch rechtseindeutig ist,
2. Auf der
Menge A = {x/x∈ N ∧ x < 11} ist die Relation
R = { (x,y) ∈ A
x A / y ≤
2x } erklärt.
a)
Stellen Sie die Relation in Form einer Wertetabelle dar.
b) Leiten Sie die
Umkehrvorschrift her und
zeichnen Sie die Umkehrrelation in ein
Koordinatensystem ein.
c) Sind Relation und Umkehrrelation Funktionen?
(Begründung!)
d) Welche der
Eigenschaften links- und
rechtstotal bzw. links- und rechtseindeutig
haben R und R-1? (Bitte nicht vorhandene
Eigenschaften begründen!)
3. a) Leiten
Sie für die Funktion f mit der Funktionsgleichung
f(x) = 2x2 - x
die Umkehrvorschrift her (Grundmenge R x R).
b)
Bestimmen Sie den größtmöglichen
Definitions- und Wertebereich,
für den eine Umkehrfunktion existiert.
4.
Gegeben ist die lineare Funktion f: x → 2 x + 1.
a)
Zeichnen Sie den
Graph von f mit Hilfe
einer Wertetabelle in ein Koordinatensystem.
b)
Leiten Sie die
Vorschrift für die
Umkehrfunktion f -1 her.
c)
Bestimmen Sie Die
Gleichung der linearen
Funktion g, die senkrecht auf f-1 steht
und durch den
Koordinatenursprung geht.
d)
Bestimmen
Sie f ∩ g.
5. Gegeben sind
die Punkte A (-2/-4), B (2/4) und C (4/-2).
a)
Bestimmen Sie die
Gleichungen der
linearen Funktionen durch je zwei der drei Punkte.
b)
Berechnen Sie die
Größe der Innenwinkel
des Dreiecks ABC.
c)
Bestimmen Sie die
Gleichung der linearen
Funktion durch den Punkt C,
die senkrecht auf AB steht.
6. Stellen Sie die
folgenden Relationen
jeweils in einem Koordinatensystem dar und geben Sie an, um
welche
Vorschriften es sich dabei
handelt.
a)
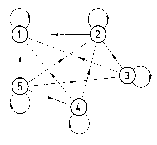
b)
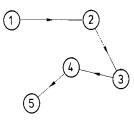
c)
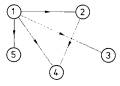
d)
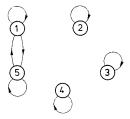
7. Die Punkte
A, B und C (vgl. Aufg. 5) sind Punkte des Graphen einer quadratischen
Funktion f.
a) Bestimmen Sie die
Funktionsgleichung.
b) Prüfen Sie
mittels Diskriminante, ob
Nullstellen vorhanden sind und
c) berechnen Sie die
Nullstellen ggf. und
den Ordinatenabschnitt.
8. Gegeben ist
die folgende Aussageform: Für alle natürlichen Zahlen
n gilt, dass
die Summe der ersten n natürlichen Zahlen 0,5 * n * (1 + n)
beträgt.
a) Schreiben Sie diese
Aussageform mit
Hilfe des Summenzeichens ∑.
Beweisen Sie
die Aussageform.